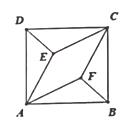
小明用四根相同长度的木条制作了一个正方形学具（如图1），测得对角线，将正方形学具变形为菱形（如图2），，则图2中对角线的长为（　　）

0 返回出卷网首页

1. 小明用四根相同长度的木条制作了一个正方形学具（如图1），测得对角线 $\text{[math]}$ ，将正方形学具变形为菱形（如图2）， $\text{[math]}$ ，则图2中对角线 $\text{[math]}$ 的长为（　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

勾股定理; 菱形的性质; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 小明用四根长度相等的木条制作了能够活动的菱形学具，他先活动学具成为图（1）所示的菱形，并测得 $\text{[math]}$ ，接着活动学具成为图（2）所示的正方形，并测得对角线 $\text{[math]}$ ，则图（1）中菱形的对角线 $\text{[math]}$ 长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. 10 D. 15

单选题容易

2. 小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得 $\text{[math]}$ ，对角线 $\text{[math]}$ ，接着活动学具成为图2所示正方形，则图2中对角线 $\text{[math]}$ 的长为（）

A. 5 B. $\text{[math]}$ C. 10 D. 15

单选题容易

3. 如图，菱形 $\text{[math]}$ 的两对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易