1.
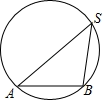
如图,点  在圆上,若弦
在圆上,若弦  的长度等于圆半径的
的长度等于圆半径的  倍,则
倍,则  的度数是( ).
的度数是( ).
A.
22.5°
B.
30°
C.
45°
D.
60°
【考点】
勾股定理的逆定理;
圆周角定理;