1.
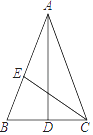
将两个底边相等的等腰三角形按照如图所示的方式拼接在一起(隐藏互相重合的底边)的图形俗称为“筝形”.假如“筝形”下个定义,那么下面四种说法中,你认为最能够描述“筝形”特征的是( )

A.
有两组邻边相等的四边形称为“筝形”
B.
有两组对角分别相等的四边形称为“筝形”
C.
两条对角线互相垂直的四边形称为“筝形”
D.
以一条对角线所在直线为对称轴的四边形称为“筝形”
【考点】
等腰三角形的性质;
轴对称的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练