1.
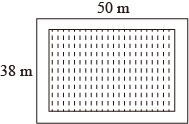
某地计划对矩形广场进行扩建改造,如图,原广场长50m,宽40m,要求扩建后的矩形广场的长与宽的比为3:2.扩充区域的扩建费用为每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用为每平方米100元.如果计划总费用为642000元,那么扩建后广场的长和宽分别是多少m?

【考点】
一元二次方程的应用-几何问题;