1.
如图所示,在平面直角坐标系中,Rt△OBC的两条直角边分别落在x轴、y轴上,且OB=1,OC=3,将△OBC绕原点O顺时针旋转90°得到△OAE,将△OBC沿y轴翻折得到△ODC,AE与CD交于点F.
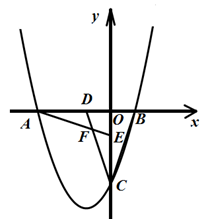
(1)若抛物线过点A、B、C, 求此抛物线的解析式;
(2)求△OAE与△ODC重叠的部分四边形ODFE的面积;
(3)点M是第三象限内抛物线上的一动点,点M在何处时△AMC的面积最大?最大面积是多少?求出此时点M的坐标.

(1)若抛物线过点A、B、C, 求此抛物线的解析式;
(2)求△OAE与△ODC重叠的部分四边形ODFE的面积;
(3)点M是第三象限内抛物线上的一动点,点M在何处时△AMC的面积最大?最大面积是多少?求出此时点M的坐标.
【考点】
二次函数图象的几何变换;
基础巩固
能力提升
变式训练
拓展培优
真题演练



