1.
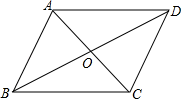
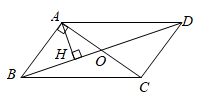
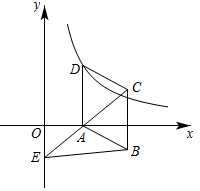
如图,请用三种不同方法将平行四边形ABCD分割成四个面积相等的三角形.(作图工具不限,保留作图痕迹,不写作法.)

【考点】
三角形的面积;
平行四边形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练