1.
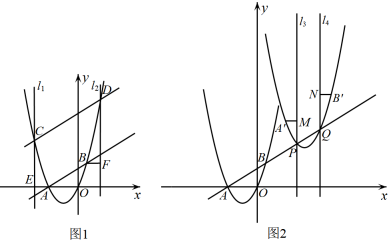
如图1,抛物线C:y=ax2+bx经过点A(﹣4,0)、B(﹣1,3)两点,G是其顶点,将抛物线C绕点O旋转180°,得到新的抛物线C′.

(1)
求抛物线C的函数解析式及顶点G的坐标;
(2)
如图2,直线l:y=kx  经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;
(3)
如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.
经过点A,D是抛物线C上的一点,设D点的横坐标为m(m<﹣2),连接DO并延长,交抛物线C′于点E,交直线l于点M,若DE=2EM,求m的值;
(3)
如图3,在(2)的条件下,连接AG、AB,在直线DE下方的抛物线C上是否存在点P,使得∠DEP=∠GAB?若存在,求出点P的横坐标;若不存在,请说明理由.
【考点】
二次函数图象的几何变换;
二次函数与一次函数的综合应用;
能力提升
真题演练