1.
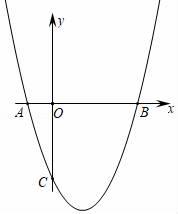
抛物线y=ax2+bx﹣3与x轴交于A , B两点,与y轴交于点C , 且OB=OC=3OA , 求抛物线的解析式( )
A.
y=x2﹣2x﹣3
B.
y=x2﹣2x+3
C.
y=x2﹣2x﹣4
D.
y=x2﹣2x﹣5
【考点】
待定系数法求二次函数解析式;




