1.
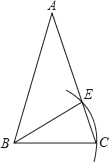
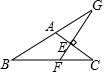
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点G.若EG=3,则BF=( )
A.
 B.
3
C.
2
D.
4
B.
3
C.
2
D.
4
【考点】
等腰三角形的判定与性质;
含30°角的直角三角形;