1.
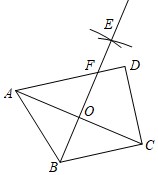
如图,∠ACB=90°,AC=BC,CD平分∠ACB,点D,E关于CB对称,连接EB并延长,与AD的延长线交于点F,连接DE,CE.对于以下结论:
①DE垂直平分CB;②AD=BE;③∠F不一定是直角;④EF2+DF2=2CD2 .
其中正确的是( )

A.
①④
B.
②③
C.
①③
D.
②④
【考点】
平行线的性质;
全等三角形的判定与性质;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练