1.
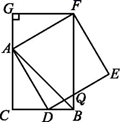
如图,CB=CA,∠ACB=90°,点D在边BC上(与点B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC.其中所有正确结论的序号是.
【考点】
矩形的判定与性质;
相似三角形的判定与性质;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练