1.
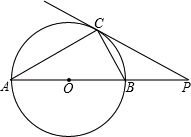
如图,△ABC内接于⊙O .

(1)
如图①,连接OA , OC , 若  ,求
,求  的度数;
(2)
如图②,直径CD的延长线与过点A的切线相交于点P . 若
的度数;
(2)
如图②,直径CD的延长线与过点A的切线相交于点P . 若  ,⊙O的半径为2,求AD , PD的长.
,⊙O的半径为2,求AD , PD的长.
【考点】
等边三角形的判定与性质;
含30°角的直角三角形;
圆周角定理;
切线的性质;
能力提升
真题演练