1.
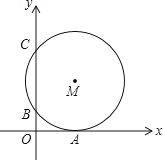
如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为(﹣3,2),则该圆弧所在圆心坐标是( )

A.
(0,0)
B.
(﹣2,1)
C.
(﹣2,﹣1)
D.
(0,﹣1)
【考点】
坐标与图形性质;
垂径定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练