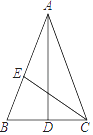
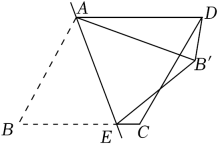
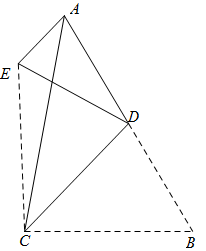
AD是△ABC的高，AC=2 ，AD=4，把△ADC沿着直线AD对折，点C落在点E的位置，如果△ABE是等腰三角形，那么线段BE的长度为（）

0 返回出卷网首页

1. AD是△ABC的高，AC=2 $\text{[math]}$ ，AD=4，把△ADC沿着直线AD对折，点C落在点E的位置，如果△ABE是等腰三角形，那么线段BE的长度为（）

A. 2 $\text{[math]}$ B. 2 $\text{[math]}$ 或5 C. 2 $\text{[math]}$ D. 5

【考点】

等腰三角形的性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是（）

A. 20° B. 35° C. 40° D. 70°

单选题容易

2. 等腰三角形的一个内角为 $\text{[math]}$ ，则另外两个内角的度数分别是（）

A. $\text{[math]}$ B. $\text{[math]}$ 或 $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$ 或 $\text{[math]}$

单选题容易

3. 如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG的度数为（）

A. 40° B. 45° C. 50° D. 60°

单选题容易