1.
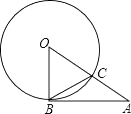
如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )

A.
2
B.
 ﹣
﹣  π
C.
1
D.
π
C.
1
D.
 +
+  π
π
【考点】
切线的性质;
扇形面积的计算;