1.
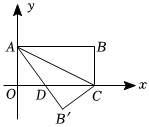
如图,在直角坐标系,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(3,1),将矩形沿对角线BO翻折,C点落在D点的位置,且BD交x轴于点E.那么点D的坐标为.

【考点】
坐标与图形性质;
矩形的性质;
翻折变换(折叠问题);
基础巩固
能力提升
变式训练
拓展培优
真题演练