1.
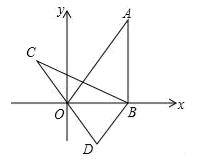
如图所示,在  中,
中,  ,
,  ,
,  ,将
,将  绕点C逆时针旋转
绕点C逆时针旋转  得到
得到  ,连接
,连接  ,
,  ,并延长
,并延长  交
交  于点D,则
于点D,则  的长为.
的长为.

【考点】
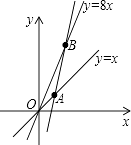
待定系数法求一次函数解析式;
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练