1.
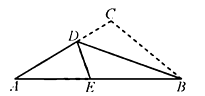
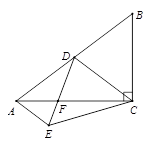
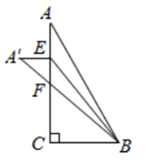
如图,在Rt△ABC中,∠C=90°,点E在AC边上.将∠A沿直线BE翻折,点A落在点A'处,连接A'B,交AC于点F.若A'E⊥AE,cosA=  ,则
,则  ( )
( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
翻折变换(折叠问题);
相似三角形的判定与性质;
等腰直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练