1.
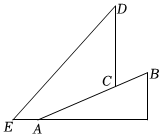
如图,直立于地面上的电线杆  ,在阳光下落在水平地面和坡面上的影子分别是
,在阳光下落在水平地面和坡面上的影子分别是  、
、  ,测得
,测得  米,
米,  米,
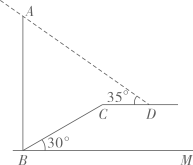
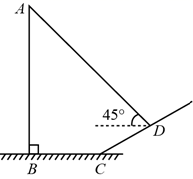
米,  ,在
,在  处测得电线杆顶端
处测得电线杆顶端  的仰角为
的仰角为  ,则电线杆
,则电线杆  的高度约为米.(参考数据:
的高度约为米.(参考数据:  ,
,  ,结果按四舍五入保留一位小数)
,结果按四舍五入保留一位小数)
【考点】
勾股定理;
解直角三角形的实际应用﹣仰角俯角问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练