1.
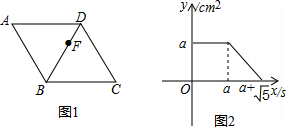
如图1,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B,△FBC的面积y(cm2)随时间x(s)变化的关系图象,则a的值为( )

A.
 B.
2
C.
B.
2
C.
 D.
2
D.
2
【考点】
勾股定理;
菱形的性质;
动点问题的函数图象;
基础巩固
能力提升
变式训练
拓展培优
真题演练