1.
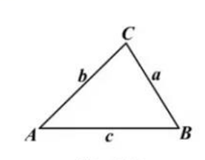
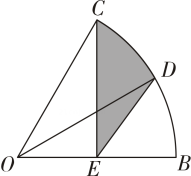
“莱洛三角形”是机械学家莱洛研究发现的一种曲边三角形,转子发动机的设计就是利用了莱洛三角形.它是分别以正三角形的顶点为圆心,以其边长为半径作弧形成的图形,如图2所示.若正三角形的边长为3,则该“莱洛三角形”的面积为( )

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形的面积;
扇形面积的计算;