0 返回出卷网首页
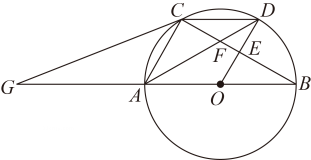
1. 已知：如图，AO是⊙O的半径，AC为⊙O的弦，点F为的中点，OF交AC于点E，AC=10，EF=3·

(1) 求AO的长；
(2) 过点C作CD⊥AO，交AO延长线于点D，求OD的长·
【考点】
勾股定理; 垂径定理; 解直角三角形;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 在Rt△ABC中，∠BAC=90°，BC=10，tan∠ABC= ，点O是AB边上动点，以O为圆心，OB为半径的⊙O与边BC的另一交点为D ， 过点D作AB的垂线，交⊙O于点E ， 联结BE、AE

(1) 如图（1），当AE∥BC时，求⊙O的半径长；
(2) 设BO=x ， AE=y ， 求y关于x的函数关系式，并写出定义域；
(3) 若以A为圆心的⊙A与⊙O有公共点D、E ， 当⊙A恰好也过点C时，求DE的长．
综合题 困难
2. 如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．

(1) 求证：∠ABD=2∠BDC；
(2) 过点C作CH⊥AB于H，交AD于E，求证：EA=EC；
(3) 在（2）的条件下，若OH=5，AD=24，求线段DE的长
综合题 普通
3. 已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C，D（如图）．

(1) 求证：AC=BD；
(2) 若大圆的半径R=10，小圆的半径r=8，且圆O到直线AB的距离为6，求AC的长．
综合题 普通