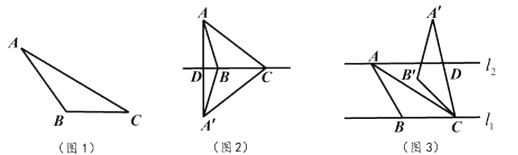
1.
如图,在 中,
中, ,
,  , 延长
, 延长 至点P,使
至点P,使 , 将线段
, 将线段 绕点C逆时针旋转角
绕点C逆时针旋转角 得到
得到 , 连结
, 连结 ,
,  .
.

(1)
当 时,点
时,点 到直线
到直线 的距离为;
(2)
当
的距离为;
(2)
当 时,点
时,点 到直线
到直线 的距离为.
的距离为.
【考点】
含30°角的直角三角形;
勾股定理;
旋转的性质;