如图（1），∠AOB=45°，点P、Q分别是边OA，OB上的两点，且OP=2cm．将∠O沿PQ折叠，点O落在平面内点C处．

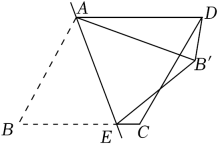
1. 如图（1），∠AOB=45°，点P、Q分别是边OA，OB上的两点，且OP=2cm．将∠O沿PQ折叠，点O落在平面内点C处．

(1) ①当PC∥QB时，OQ=；

(2) 当折叠后重叠部分为等腰三角形时，求OQ的长．

【考点】

等腰三角形的性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

综合题困难

综合题困难

例1 等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.（答案： $\text{[math]}$ ）

例2 等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.（答案： $\text{[math]}$ 或 $\text{[math]}$ 或 $\text{[math]}$ ）

张老师启发同学们进行变式，小敏编了如下一题：

变式等腰三角形 $\text{[math]}$ 中， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

综合题普通