1.
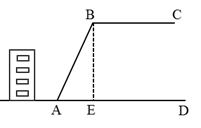
如图,平地上种植树木的株距(相邻两树间的水平距离)为4m,如果在坡比为3:4的山坡上种树,株距也为4m,那么相邻两树间的坡面距离为多少?

【考点】
勾股定理;
解直角三角形的实际应用﹣坡度坡角问题;