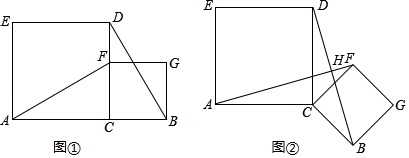
（1）如图①，在正方形内有一点，，点是的中点，且．连接，求的最小值；（2）如图②，某小区有五栋楼，刚好围成五边形，米，米，在小区内部建立一个老年活动中心，满足栋楼到栋楼之间的距离与栋楼到老年活动中心的距离相等（即，过点作于点，老年活动中心，，围成直角三角形．在的内心建立一个餐厅，现修建一条小路，使得栋楼的居民到餐厅的距离最小，请问是否存在最小距离？若存在，求出的最小值；若不存在，请说明理由．

0 返回出卷网首页

1. （1）如图①，在正方形 $\text{[math]}$ 内有一点 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 的中点，且 $\text{[math]}$ ．连接 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值；

（2）如图②，某小区有五栋楼，刚好围成五边形 $\text{[math]}$ ， $\text{[math]}$ 米， $\text{[math]}$ 米，在小区内部建立一个老年活动中心 $\text{[math]}$ ，满足 $\text{[math]}$ 栋楼到 $\text{[math]}$ 栋楼之间的距离与 $\text{[math]}$ 栋楼到老年活动中心 $\text{[math]}$ 的距离相等（即 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，老年活动中心 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 围成直角三角形 $\text{[math]}$ ．在 $\text{[math]}$ 的内心建立一个餐厅 $\text{[math]}$ ，现修建一条小路，使得 $\text{[math]}$ 栋楼的居民到餐厅 $\text{[math]}$ 的距离最小，请问是否存在最小距离 $\text{[math]}$ ？若存在，求出 $\text{[math]}$ 的最小值；若不存在，请说明理由．

【考点】

勾股定理; 正方形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 【问题背景】

如图 $\text{[math]}$ ， $\text{[math]}$ 是一张等腰直角三角形纸板， $\text{[math]}$ ， $\text{[math]}$ 取 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 中点进行第 $\text{[math]}$ 次剪取，记所得正方形面积为 $\text{[math]}$ ，如图 $\text{[math]}$ ，在余下的 $\text{[math]}$ 和 $\text{[math]}$ 中，分别剪取正方形，得到两个相同的正方形，称为第 $\text{[math]}$ 次剪取，并记这两个正方形面积和为 $\text{[math]}$ 如图 $\text{[math]}$ .

【问题探究】

（1） $\text{[math]}$ ______ ；

（2）如图 $\text{[math]}$ ，再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第 $\text{[math]}$ 次剪取，并记这四个正方形面积和为 $\text{[math]}$ 继续操作下去 $\text{[math]}$ ，则第 $\text{[math]}$ 次剪取时， $\text{[math]}$ ______ ；第 $\text{[math]}$ 次剪取时， $\text{[math]}$ ______ ．

【拓展延伸】

在第 $\text{[math]}$ 次剪取后，余下的所有小三角形的面积之和为______ ．

实践探究题容易

2. 明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地．送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千 $\text{[math]}$ 静止的时候，踏板离地高一尺（ $\text{[math]}$ 尺），将它往前推进两步（ $\text{[math]}$ 尺），此时踏板升高离地五尺（ $\text{[math]}$ 尺），求秋千绳索（ $\text{[math]}$ 或 $\text{[math]}$ ）的长度．

综合题容易

3. 在△ABC中，∠C=30°，AC=4cm，AB=3cm，求BC的长.

解答题容易