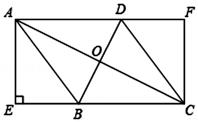
如图，某大厦离地米的处突发火情，消防车立即赶到距大厦米的处，升起云梯到发生火灾的处，已知云梯长米，求云梯底部距离地面的高度的长．

0 返回出卷网首页

1. 如图，某大厦离地 $\text{[math]}$ 米的 $\text{[math]}$ 处突发火情，消防车立即赶到距大厦 $\text{[math]}$ 米的 $\text{[math]}$ 处，升起云梯到发生火灾的 $\text{[math]}$ 处，已知云梯 $\text{[math]}$ 长 $\text{[math]}$ 米，求云梯底部距离地面的高度 $\text{[math]}$ 的长．

【考点】

勾股定理; 矩形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题容易

1. 如图，两根直立的竹竿相距6m，高分别为4m和7m，求两竹竿顶端间的距离AD．

解答题容易

2. 如图，将一组邻边长分别为2和6的两个矩形 $\text{[math]}$ 和矩形 $\text{[math]}$ 拼成“ $\text{[math]}$ ”形图案，则线段 $\text{[math]}$ 的长为．

填空题容易

3. 如图，小明准备建一个鲜花大棚，棚宽 $\text{[math]}$ 米，高 $\text{[math]}$ 米，且 $\text{[math]}$ ，长 $\text{[math]}$ 米，棚的斜面用矩形玻璃 $\text{[math]}$ 遮盖，不计墙的厚度，请计算矩形玻璃 $\text{[math]}$ 的面积．

综合题容易