1.
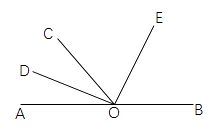
如图,直线AB、CD相交于点O,过点O作OE⊥CD.

(1)如图1,将射线OB沿着直线CD翻折得到射线OF,即∠BOD=∠FOD.求证:OE平分∠AOF;
(2)如图2,在(1)的条件下,过点O作OG⊥AB,当∠FOG:∠AOE=2:3时,求∠COG的度数.
【考点】
角的运算;
垂线的概念;
角平分线的概念;
基础巩固
能力提升
变式训练
拓展培优