1.
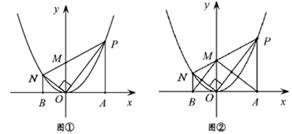
如图,在正方形网格中,每个小正方形的边长均为1,点A,B,C,D,P都在格点上,连接AP,CP,CD,则∠PAB-∠PCD=.

【考点】
等腰三角形的判定;
勾股定理的逆定理;
基础巩固
能力提升
变式训练
拓展培优