1.
如图,在△ABC中,CD⊥AB,垂足为点D.以AB为直径的半⊙O分别与
AC,CD相交于点E,F,连接AF,EF.
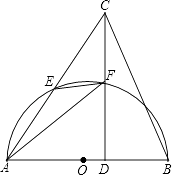
(1)
求证:∠AFE=∠ACD;
(2)
若CE=4,CB=4  ,tan∠CAB=
,tan∠CAB=  ,求FD的长.
,求FD的长.
【考点】
勾股定理;
圆周角定理;
解直角三角形;
能力提升
真题演练