1.
在学习矩形的过程中,小明遇到了一个问题:在矩形 中,
中, 是
是 边上的一点,试说明
边上的一点,试说明 的面积与矩形
的面积与矩形 的面积之间的关系.他的思路是:首先过点
的面积之间的关系.他的思路是:首先过点 作
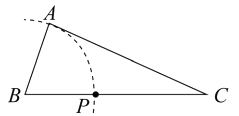
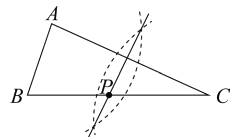
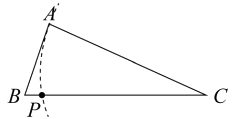
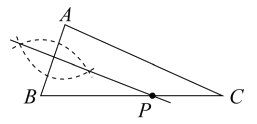
作 的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:
的垂线,将其转化为证明三角形全等,然后根据全等三角形的面积相等使问题得到解决.请根据小明的思路完成下面的作图与填空:

证明:用直尺和圆规,过点作
的垂线
, 垂足为
(只保留作图㾗迹).
在和
中,
∵ ,
∴ .
又 ,
∴__________________①
∵ ,
∴__________________②
又__________________③
∴ .
同理可得__________________④
∴ .
【考点】
尺规作图-垂直平分线;
基础巩固
能力提升
变式训练
拓展培优
真题演练