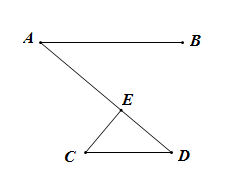
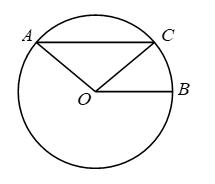
将一个直角三角形纸板放置在锐角上，使该直角三角形纸板的两条直角边，分别经过点M，N．【发现】（1）如图1，若点A在内，当时，则；（2）如图2，若点A在内，当时，；【探究】若点A在内，请你判断，和之间满足怎样的数量关系，并写出理由；【应用】如图3，点A在内，过点P作直线，若，求的度数；【拓展】如图4，当点A在外，请直接写出，和之间满足的数量关系．

0 返回出卷网首页

1. 将一个直角三角形纸板 $\text{[math]}$ 放置在锐角 $\text{[math]}$ 上，使该直角三角形纸板的两条直角边 $\text{[math]}$ ， $\text{[math]}$ 分别经过点M，N．

【发现】

（1）如图1，若点A在 $\text{[math]}$ 内，当 $\text{[math]}$ 时，则 $\text{[math]}$ ；

（2）如图2，若点A在 $\text{[math]}$ 内，当 $\text{[math]}$ 时， $\text{[math]}$ ；

【探究】

若点A在 $\text{[math]}$ 内，请你判断 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 之间满足怎样的数量关系，并写出理由；

【应用】

如图3，点A在 $\text{[math]}$ 内，过点P作直线 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

【拓展】

如图4，当点A在 $\text{[math]}$ 外，请直接写出 $\text{[math]}$ ， $\text{[math]}$ 和 $\text{[math]}$ 之间满足的数量关系．

【考点】

平行线的性质; 三角形内角和定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，在△ABC中，∠A＝45°，CD平分∠ACB交AB于点D， $\text{[math]}$ ， ∠ADE＝65°，求∠CDE的度数．

解答题容易

2. 如图，B处在A处南偏西39°方向，C处在A处南偏东20°方向，C处在B处的北偏东78°方向，求 $\text{[math]}$ 的度数．

解答题容易

3. 如图，△ABC中，∠C=45°，∠A=55°，BE是△ABC角平分线，点D在AB上，且DE∥BC，求∠DEB的度数．

解答题容易

1. 综合与探究，问题情境：综合实践课上，数学老师组织同学们开展了探究三个角之间数量关系的数学活动．已知：三角形的内角和为 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 分别与直线 $\text{[math]}$ 、 $\text{[math]}$ 交于点F、G．

(1) 如图1，点E在线段 $\text{[math]}$ 上， $\text{[math]}$ ，求 $\text{[math]}$ 的度数？

(2) 如图2， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线， $\text{[math]}$ 是 $\text{[math]}$ 的角平分线所在直线， $\text{[math]}$ 与 $\text{[math]}$ 交于点Q，试探究 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系？

(3) 如图3， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点K，交 $\text{[math]}$ 于点I，且 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数？

实践探究题困难

2. 探究题

学习近平行线的性质与判定之后，我们发现借助构造平行线的方法可以帮我们解决许多问题．

(1) 小明遇到了下面的问题：如图1， $\text{[math]}$ ，点P在 $\text{[math]}$ 、 $\text{[math]}$ 内部，探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的关系 $\text{[math]}$ 小明过点P作 $\text{[math]}$ 的平行线，可证 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系是：

$\text{[math]}$ ．

(2) 如图2，若 $\text{[math]}$ ，点P在AC、BD外部， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的数量关系是否发生变化？

请你补全下面的证明过程．

过点P作 $\text{[math]}$ ．

$\text{[math]}$

$\text{[math]}$ $\text{[math]}$

$\text{[math]}$

$\text{[math]}$ ．

(3) 随着以后的学习你还会发现平行线的许多用途．

试构造平行线解决以下问题：

已知：如图3，三角形ABC ，求证： $\text{[math]}$ ．

实践探究题困难

3. 如图1，自行车尾灯是由塑料罩片包裹的若干个小平面镜组成，利用平面镜反射光线，以提醒后方车辆注意．小亮所在学习小组对其工作原理进行探究，发现以下规律：如图2， $\text{[math]}$ 为平面镜， $\text{[math]}$ 分别为入射光线和反射光线，则 $\text{[math]}$ ．请继续以下探究：

(1) 探究反射规律

①如图3， $\text{[math]}$ ，则 $\text{[math]}$ ▲ (用含 $\text{[math]}$ 的代数式表示)．

②若光线 $\text{[math]}$ ，判断 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由．

(2) 模拟应用研究

在行驶过程中，后车驾驶员平视前方，且视点 $\text{[math]}$ 会高于反射点 $\text{[math]}$ (如图4)，因此小亮认为反射光线 $\text{[math]}$ 应与水平视线 $\text{[math]}$ 成一定角度．学习小组设计了如图5所示的模拟实验装置，使入射光线 $\text{[math]}$ ，当 $\text{[math]}$ 与 $\text{[math]}$ 所成夹角为 $\text{[math]}$ 时，求 $\text{[math]}$ 的度数．

实践探究题普通

1. 如图，在 $\text{[math]}$ 中，点D、E分别在 $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

2. 如图，若 $\text{[math]}$ ，且 $\text{[math]}$ 于点C，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

填空题普通

3. 如图，在直角三角形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 则 $\text{[math]}$ 的度数为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

1. 在科学实验课上，小明发现： $\text{[math]}$ ．光线在不同介质中的传播速度是不一样的，当光线从一种介质射向另一种介质时，折射现象便会发生；2．经过实验，小明还发现凸透镜能让与主光轴平行的光线汇聚在主光轴上的某一点．基于这些发现，小明设计了以下三个问题：

(1) 如图 $\text{[math]}$ ，这是一块玻璃的 $\text{[math]}$ ， $\text{[math]}$ 两面，且 $\text{[math]}$ ．现有一束光线 $\text{[math]}$ 从玻璃射向空气时发生折射，光线变成 $\text{[math]}$ ， $\text{[math]}$ 为射线 $\text{[math]}$ 上的一点．已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(2) 如图 $\text{[math]}$ ，箭头所画的是光线的方向， $\text{[math]}$ 是凸透镜的焦点， $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(3) 联想拓展：如图 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 的邻补角 $\text{[math]}$ 的角平分线与 $\text{[math]}$ 的邻补角 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，请直接写出 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 的数量关系．

解答题普通

2. 如图，已知 $\text{[math]}$ ，直线 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．点 $\text{[math]}$ 是线段 $\text{[math]}$ 上一点， $\text{[math]}$ ， $\text{[math]}$ 分别在射线 $\text{[math]}$ ， $\text{[math]}$ 上，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 如图1，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ________ $\text{[math]}$ ， $\text{[math]}$ ________ $\text{[math]}$ ．

(2) 如图2， $\text{[math]}$ 的角平分线与 $\text{[math]}$ 的角平分线相交于点 $\text{[math]}$ ．

①求 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系，并说明理由；

②若 $\text{[math]}$ ， $\text{[math]}$ ，将直线 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度顺时针旋转，同时射线 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度逆时针旋转，当直线 $\text{[math]}$ 首次落到 $\text{[math]}$ 上时，整个运动停止．在运动过程中，经过 $\text{[math]}$ 秒后直线 $\text{[math]}$ 恰好平行于 $\text{[math]}$ ，请直接写出所有满足条件的 $\text{[math]}$ 的值．