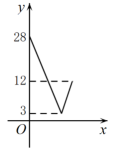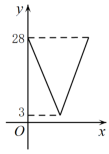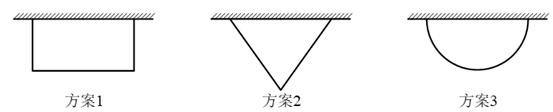
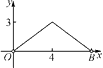
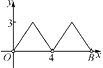
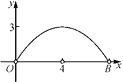
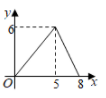
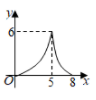
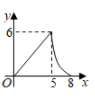
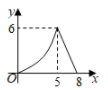
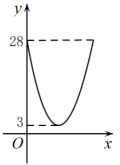
下面的三个问题中都有两个变量：①边长为的正方形纸片中间剪去一个边长为x dm的正方形纸片，剩下纸片的面积y与x；②用长为的绳子围成一个矩形，矩形的面积y与一边长x；③某种商品的价格为4元，准备进行两次降价，如果每次降价的百分率都是x，经过两次降价后的价格y与x．其中变量y与x之间的函数关系可以利用如图所示的图象表示的是（）．

1. 如图，已知抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴分别交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，将抛物线 $\text{[math]}$ 向上平移得到 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交抛物线 $\text{[math]}$ 于点 $\text{[math]}$ ，如果由抛物线 $\text{[math]}$ 、 $\text{[math]}$ 、直线 $\text{[math]}$ 及 $\text{[math]}$ 轴所围成的阴影部分的面积为 $\text{[math]}$ ，则抛物线 $\text{[math]}$ 的函数表达式为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 如图，将一根长 $\text{[math]}$ 的铁丝弯成一个长方形(铁丝正好全部用完且无损耗)，设这个长方形的一边长为 $\text{[math]}$ ，它的面积为 $\text{[math]}$ ，则y与x之间的函数关系式为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 用绳子围成周长为10（m）的矩形，记矩形的一边长为x（m），面积为S（m²）．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数关系是（）

A. 一次函数关系 B. 二次函数关系 C. 反比例函数关系 D. 正比例函数关系

单选题容易

1. 如图，人民医院在某流感高发时段，用防护隔帘布临时搭建了一隔离区，隔离区一面靠长为 $\text{[math]}$ 的墙，隔离区分成两个区域，中间也用防护隔帘布隔开．已知整个隔离区所用防护隔帘布总长为 $\text{[math]}$ ，如果隔离区出入口的大小不计，并且隔离区靠墙的一面不能超过墙长，小明认为：隔离区的最大面积为 $\text{[math]}$ ；小亮认为：隔离区的面积可能为 $\text{[math]}$ ．你认为他们俩的说法是（）

A. 小明正确，小亮错误 B. 小明错误，小亮正确 C. 两人均正确 D. 两人均错误

单选题普通

2. 如图，菱形ABCD的对角线AC，BD相交于点O，AC＝6，BD＝8，动点P从点B出发，沿着B－A－D在菱形ABCD的边上运动，运动到点D停止，点P′是点P关于BD的对称点，PP′交BD于点M，若BM＝x，△OPP′的面积为y，则y与x之间的函数图象大致为（）

单选题普通

3. 如图，一边靠校园围墙，其他三边用总长为40米的铁栏杆围成一个矩形花圃，设矩形ABCD的边AB为x米，面积为S平方米，要使矩形ABCD面积最大，则x的长为（　　）

A. 10米 B. 15米 C. 20米 D. 25米

单选题普通

1. 在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB，CD，以点B为坐标原点，直线BD为x轴建立平面直角坐标系，得到图1．已知电线杆之间的电线可近似地看成抛物线y＝ $\text{[math]}$ x²﹣ $\text{[math]}$ x+30．

（1）求电线杆AB和线段BD的长．

（2）因实际需要，电力公司在距离AB为30米处增设了一根电线杆MN（如图2），左边抛物线F₁的最低点离MN为10米，离地面18米，求MN的长．

（3）将电线杆MN的长度变为30米，调整电线杆MN在线段BD上的位置，使右边抛物线F₂的二次项系数始终是 $\text{[math]}$ ，设电线杆MN距离AB为m米，抛物线F₂的最低点离地面的距离为k米，当20≤k≤25时，求m的取值范围．

解答题普通

2. 根据以下素材，探索完成任务．

如何设计打印图纸方案？
素材1	如图1，正方形 $\text{[math]}$ 是一张用于 $\text{[math]}$ 打印产品的示意图，它由三个区块（Ⅰ，Ⅱ，Ⅲ）构成．已知 $\text{[math]}$ ，点E，F分别在 $\text{[math]}$ 和 $\text{[math]}$ 上，且 $\text{[math]}$ ，设 $\text{[math]}$ $\text{[math]}$ ．
素材2	为了打印精准，拟在图2中的 $\text{[math]}$ 边上设置一排间距为1cm的定位坐标（B为坐标原点），计算机可根据点E的定位坐标精准打印出图案．
问题解决
任务1	确定关系	用x的代数式表示：区域Ⅰ的面积＝______；区域Ⅱ的面积＝______．
任务2	拟定方案	为了美观，拟将区域Ⅲ分割为甲、乙两个三角形区域，并要求区域乙是含 $\text{[math]}$ 边的三角形，求所有方案中乙的面积或者函数表达式．
任务3	优化设计	经调查发现当 $\text{[math]}$ 且x为整数时，此时称E点为合格定位点．当区域乙的面积最小时，合格定位点E点为最佳定位点，求出最佳定位点E的坐标．

计算题普通

3. 已知：如图，用长为18m的篱笆（3AB+BC），围成矩形花圃．一面利用墙（墙足够长），则围成的矩形花圃ABCD的占地面积最大为m² ．

填空题普通

1. 【生活情境】

为美化校园环境，某学校根据地形情况，要对景观带中一个长 $\text{[math]}$ ，宽 $\text{[math]}$ 的长方形水池 $\text{[math]}$ 进行加长改造（如图①，改造后的水池 $\text{[math]}$ 仍为长方形，以下简称水池1），同时，再建造一个周长为 $\text{[math]}$ 的矩形水池 $\text{[math]}$ （如图②，以下简称水池2）．

【建立模型】

如果设水池 $\text{[math]}$ 的边 $\text{[math]}$ 加长长度 $\text{[math]}$ 为 $\text{[math]}$ ，加长后水池1的总面积为 $\text{[math]}$ ，则 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式为： $\text{[math]}$ ；设水池2的边 $\text{[math]}$ 的长为 $\text{[math]}$ ，面积为 $\text{[math]}$ ，则 $\text{[math]}$ 关于 $\text{[math]}$ 的函数解析式为： $\text{[math]}$ ，上述两个函数在同一平面直角坐标系中的图像如图③．