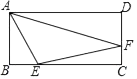
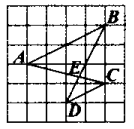
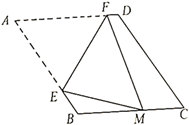
【特例感知】如图1，在中，，，平分，交于点．求证：．【性质探究】如图2，在中，平分交于点．求证：．【应用迁移】如图3，在中，，平分交于点，，垂足为点．若，，点在的延长线上，当为何值时，与相似．

0 返回出卷网首页

1. 【特例感知】如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．求证： $\text{[math]}$ ．

【性质探究】如图2，在 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ．求证： $\text{[math]}$ ．

【应用迁移】如图3，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ，垂足为点 $\text{[math]}$ ．若 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，当 $\text{[math]}$ 为何值时， $\text{[math]}$ 与 $\text{[math]}$ 相似．

【考点】

勾股定理; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题困难

1. 某数学兴趣小组在测量学校旗杆的高度时，让一名同学直立在点F处，手拿一块直角三角板CDE，保持斜边CE与地面BF平行，延长CE交AB于点G，如图，并沿着射线CD的方向观察，刚好看到旗杆的顶端A点，已知该同学的身高CF为1.6米，点F到旗杆底端的距离BF为12米，CE＝0.5m，CD＝0.4m，求旗杆AB的高度．

解答题容易

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 于点D， $\text{[math]}$ ，求 $\text{[math]}$ 和 $\text{[math]}$ ．

计算题容易

3. 已知在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 的中点， $\text{[math]}$ ，垂足为 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ．

（1）求 $\text{[math]}$ 的度数；

（2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

解答题容易