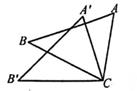
在△ABC中，AC＝4，BC＝2，AB=2 ，以AB为边在△ABC外作等腰直角△ABD，连接CD，则CD=．

0 返回出卷网首页

1. 在△ABC中，AC＝4，BC＝2，AB=2 $\text{[math]}$ ，以AB为边在△ABC外作等腰直角△ABD，连接CD，则CD=．

【考点】

三角形全等及其性质; 勾股定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 图中的小正方形边长都相等，若 $\text{[math]}$ ，则点 $\text{[math]}$ 可能是图中的．

填空题容易

2. 如图， $\text{[math]}$ ， $\text{[math]}$ ， E，F分别为线段 $\text{[math]}$ 和射线 $\text{[math]}$ 上的一点，若点E从点B出发向点A运动，同时点F从点B出发沿射线 $\text{[math]}$ 运动，二者速度之比为3∶7，当点E运动到点A时，两点同时停止运动．在射线AC上取一点G，使 $\text{[math]}$ 与 $\text{[math]}$ 全等，则 $\text{[math]}$ 的长为．

填空题容易

3. 如图， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在线段 $\text{[math]}$ 上以 $\text{[math]}$ 的速度由点 $\text{[math]}$ 向点 $\text{[math]}$ 运动，同时点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动，当点 $\text{[math]}$ 运动结束时，点 $\text{[math]}$ 随之结束运动，当点 $\text{[math]}$ 运动到某处时有 $\text{[math]}$ 与 $\text{[math]}$ 全等，则 $\text{[math]}$ 的运动速度是 $\text{[math]}$ ．

填空题容易