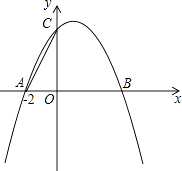
已知二次函数的图象顶点为P，且经过点．

0 返回出卷网首页

1. 已知二次函数 $\text{[math]}$ 的图象顶点为P，且经过点 $\text{[math]}$ ．

(1) 求点P坐标．

(2) 把点P先向右平移m个单位 $\text{[math]}$ ，再向上平移4m个单位得到点 $\text{[math]}$ ，若 $\text{[math]}$ 也在该函数图象上，求m的值．

【考点】

待定系数法求二次函数解析式; 坐标与图形变化﹣平移;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 小明在研究某二次函数时，函数值 $\text{[math]}$ 与自变量 $\text{[math]}$ 的部分对应值如表：

$\text{[math]}$	…	$\text{[math]}$	2	3	5	…
$\text{[math]}$	…	$\text{[math]}$	1	0	$\text{[math]}$	…

(1) 求该二次函数的表达式：

(2) 当 $\text{[math]}$ 时，该二次函数的最大值与最小值的差为2，求 $\text{[math]}$ 的值；

(3) 已知点 $\text{[math]}$ 是该二次函数图象与 $\text{[math]}$ 轴的交点，把点 $\text{[math]}$ 向下平移 $\text{[math]}$ 个单位得到点 $\text{[math]}$ ．若点 $\text{[math]}$ 向左平移 $\text{[math]}$ 个单位，将与该二次函数图象上的点 $\text{[math]}$ 重合；若点 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位，将与该二次函数图象上的点 $\text{[math]}$ 重合，求 $\text{[math]}$ 的值．

解答题普通

2. 已知抛物线 $\text{[math]}$ 过点 $\text{[math]}$ 和 $\text{[math]}$ ，求该抛物线的解析式．

解答题普通

3. 如图，一次函数 $\text{[math]}$ 的图象与坐标轴交于点A、B，二次函数 $\text{[math]}$ 的图象过A、B两点．

(1) 求二次数的表达式

(2) 已知点 $\text{[math]}$ 在对称轴上，且点 $\text{[math]}$ 位于 $\text{[math]}$ 轴上方，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求P的坐标

解答题普通