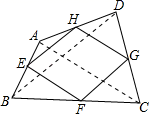
如图，E，F，G，H分别是四边形四条边的中点，要使四边形为矩形，则四边形应具备的条件是（）

0 返回出卷网首页

1. 如图，E，F，G，H分别是四边形 $\text{[math]}$ 四条边的中点，要使四边形 $\text{[math]}$ 为矩形，则四边形 $\text{[math]}$ 应具备的条件是（）

A. 一组对边平行而另一组对边不平行 B. 对角线相等 C. 对角线互相平分 D. 对角线互相垂直

【考点】

平行四边形的判定; 矩形的判定; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 下列测量方案能判定四边形台面为矩形的是（）

A. 测量得出对角线相等 B. 测量得出对角线互相平分 C. 测量得出两组对边分别相等 D. 测量得出对角线交点到四个顶点的距离相等

单选题容易

2. 一个木匠要制作矩形的踏板，他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次，就能得到矩形的踏板．这样做最直接的道理是（）

A. 有一个角是直角的四边形是矩形 B. 有一个角是直角的平行四边形是矩形 C. 对角线相等的平行四边形是矩形 D. 两组对边分别相等的四边形是矩形

单选题容易

3. 如图，在四边形 $\text{[math]}$ 中，点E，F，G，H分别是各边的中点．甲说：若四边形 $\text{[math]}$ 是平行四边形，则四边形 $\text{[math]}$ 也是平行四边形；乙说：若四边形 $\text{[math]}$ 是平行四边形，则四边形 $\text{[math]}$ 也是平行四边形．下列说法正确的是（）

A. 甲、乙都正确 B. 甲正确，乙错误 C. 甲错误，乙正确 D. 甲、乙都错误

单选题容易