1.
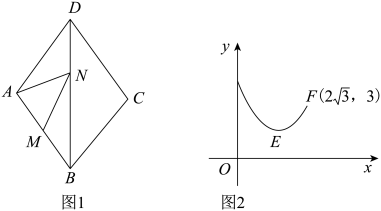
如果菱形有一条对角线等于它的边长,那么称此菱形为“完美菱形”.如图,已知“完美菱形”ABCD的边长为4,BD是它的较短对角线,点M、N分别是边AD,CD上的两个动点,且满足AM+CN=4,设△BMN的面积为S,则S的取值范围是.

【考点】
等边三角形的判定与性质;
勾股定理;
菱形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练