1.
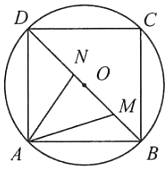
如图,正方形 由四个全等的直角三角形(
由四个全等的直角三角形( ,
,  ,
,  ,
,  )和中间一个小正方形
)和中间一个小正方形 组成,连接并延长
组成,连接并延长 , 交
, 交 ,
,  于点N,M.若
于点N,M.若 .
.

(1)比较线段大小:
. (填写“
”“
”“
”)
(2)的值等于.
【考点】
等腰三角形的判定与性质;
勾股定理;
正方形的性质;