1.
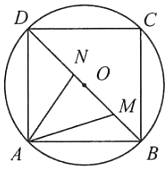
如图1,《蝶几图》是明朝的戈汕分割正方形的一种方式,以正方形为模分割为长斜(等腰梯形),右半斜和左半斜(直角梯形),小三斜,大三斜和闺(均为等腰直角三角形).现取右半斜两张,左半斜两张和小三斜两张,共6张拼成图2,若图1大正方形的边长为4,则图2阴影部分的周长是( )

A.
4
B.
 C.
C.
 D.
5
D.
5
【考点】
等腰三角形的判定与性质;
勾股定理;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练