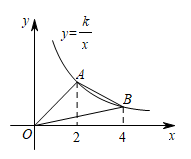
如图，A，B是反比例函数y= 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4，则△OAB的面积是（）

0 返回出卷网首页

1. 如图，A，B是反比例函数y= $\text{[math]}$ 在第一象限内的图象上的两点，且A，B两点的横坐标分别是2和4，则△OAB的面积是（）

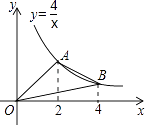
A. 4 B. 3 C. 2 D. 1

【考点】

反比例函数系数k的几何意义; 反比例函数图象上点的坐标特征; 反比例函数的一点一垂线型;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，点 $\text{[math]}$ 是反比例函数 $\text{[math]}$ 的图像上的一点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴，垂足为 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上的一点，连接 $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ 的面积为3，则 $\text{[math]}$ 的值是（　　）

A. 3 B. ﹣6 C. 6 D. ﹣3

单选题容易

2. 如图，已知点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 上， $\text{[math]}$ 轴，垂足为点 $\text{[math]}$ ，且 $\text{[math]}$ 的面积为4，则 $\text{[math]}$ 的值为（）

A. 8 B. 4 C. ﹣8 D. ﹣4

单选题容易

3. 如图，设点 $\text{[math]}$ 是函数 $\text{[math]}$ 的图象上成中心对称的两个任意点，斜边为 $\text{[math]}$ ，两条直角边分别平行于 $\text{[math]}$ 轴的直角 $\text{[math]}$ 的面积为（）

A. 2 B. 4 C. 8 D. 随点 $\text{[math]}$ 的变化而变化

单选题容易