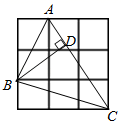
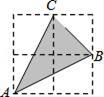
如图，在2×2正方形网格中，以格点为顶点的△ABC的面积等于，则sin∠CAB＝（）

0 返回出卷网首页

1. 如图，在2×2正方形网格中，以格点为顶点的△ABC的面积等于 $\text{[math]}$ ，则sin∠CAB＝（）

A. $\text{[math]}$ $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

三角形的面积; 等腰三角形的性质; 勾股定理; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题普通

1. 如图，在 $\text{[math]}$ 中，∠C=90°，D为AC上一点，若DA=DB=15，△ABD的面积为90，则CD的长是（）

A. 6 B. 9 C. 12 D. $\text{[math]}$

单选题容易

2. 如图，在3×3的网格中，每个小正方形的边长均为1，点A，B，C都在格点上，若BD是△ABC的高，则BD的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图，在5×5的网格中，每个格点小正方形的边长为1， $\text{[math]}$ 的三个顶点A，B，C都在网格格点的位置上，则 $\text{[math]}$ 的边 $\text{[math]}$ 上的高为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易