1.
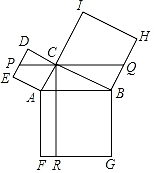
如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CR⊥FG于点R,再过点C作PQ⊥CR分别交边DE,BH于点P,Q。若QH=2PE,PQ=15,则CR的长为( )
A.
14
B.
15
C.
8
 D.
6
D.
6

【考点】
勾股定理;
平行四边形的判定与性质;
正方形的性质;
相似三角形的判定与性质;