1.
七巧板是我们祖先的一项创造,被誉为“东方魔板”.在一次数学活动课上,小明用边长为4cm的正方形纸片制作了如图所示的七巧板,并设计了下列四幅作品—“奔跑者”,其中阴影部分的面积为5cm2的是( )
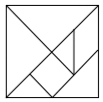
A.
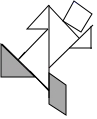 B.
B.
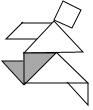 C.
C.
 D.
D.
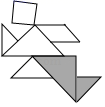
 B.
B.
 C.
C.
 D.
D.

【考点】
三角形的面积;
平行四边形的性质;
等腰直角三角形;