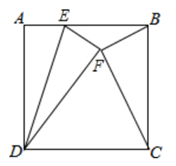
1.
如图,已知正方形 的边长为2,点E是正方形
的边长为2,点E是正方形  的边
的边  上的一点,点A关于
上的一点,点A关于 的对称点为F,若
的对称点为F,若  ,则
,则 的长为( )
的长为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
直角三角形全等的判定-HL;
正方形的性质;
翻折变换(折叠问题);

















