1.
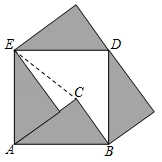
清代数学家梅文鼎在《勾股举隅》一书中,用四个全等的直角三角形拼出正方形  的方法证明了勾股定理(如图),若
的方法证明了勾股定理(如图),若  的斜边
的斜边  ,
,  ,则图中线段
,则图中线段  的长为.
的长为.
【考点】
三角形全等及其性质;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练













