1.
若  ,
,  ,
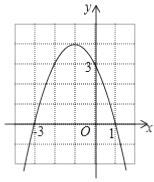
,  为二次函数
为二次函数  的图象上的三点,则
的图象上的三点,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
二次函数图象上点的坐标特征;
二次函数y=a(x-h)²+k的性质;