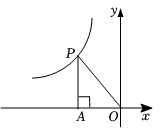
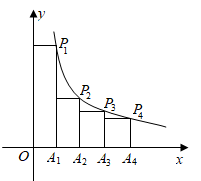
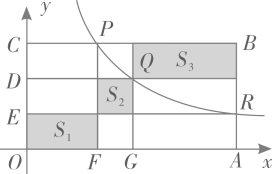
如图，已知正方形ABOC的边长为1，反比例函数y=的图象过点A，则k的值为.

0 返回出卷网首页

1. 如图，已知正方形ABOC的边长为1，反比例函数y= $\text{[math]}$ 的图象过点A，则k的值为.

【考点】

反比例函数的图象; 反比例函数系数k的几何意义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题普通

1. 如图，点P（x，y）在双曲线 $\text{[math]}$ 的图象上，PA⊥x轴，垂足为A，若S_△AOP＝2，则该反比例函数的解析式为 .

填空题容易

2. 已知反比例函数y $\text{[math]}$ （k是常数，且k≠2）的图象有一支在第三象限，那么k的取值范围是．

填空题容易

3. 已知点 M（1，2）在反比例函数 $\text{[math]}$ 的图象上，则 k＝.

填空题容易