1.
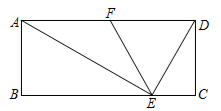
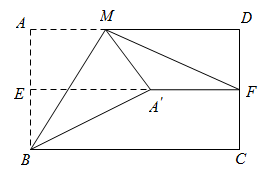
如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,点F是AD边的中点,EF=6cm,则BE=cm.

【考点】
矩形的性质;
解直角三角形;