1.
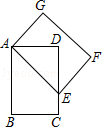
已知矩形ABCD的两边长分别为6和8,点O是矩形对角线的交点.绕点C旋转CO,当点B、O、C三点共线(在一条直线上)时,OA的长度是多少?
【考点】
勾股定理;
矩形的性质;
旋转的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练